Z会学力に差がつく｜インターエデュ

これから必要となる力　秋以降、学習ペースが速まる学校授業。

つまずきやすい学習のスタート
～小学１年生秋～
低学年で必要な学習の完成
～小学２年生秋～

高学年でつまずかないために
～小学３・４年生～
中学、そして将来必要になる力とは
～小学５・６年生～

本格的な国語学習がスタートする秋。Z会で国語学習を強力サポート。ひらがなの学習からスタートして真の国語力を養成しましょう。

たくさんの文章を書くこと。そして、自分が書いた文章に対して反応が返ってくること。これが表現力を伸ばす秘訣です。Ｚ会では、お子さまに文章を書く機会を提供するとともに、お子さまの書いた文章へ担任指導者が丁寧に添削指導していきます。


生活体験が豊かな子どもは、文章を読み解く力も優れていると言われます。不足しがちな生活体験を補うのが、本から得た知識と読書による擬似体験です。お子さまの生活体験を豊かにするさまざまな文章を、Ｚ会が精選してお届けします。	「読み聞かせ」の活動を学習の中に取り入れ、多様な文章にふれる機会を提供します。お子さまだけでは読みこなせない内容の文章も、親子でいっしょに読むことで、理解を深めることができます。

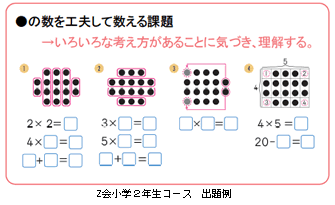
２年生の秋からは【かけ算九九】の学習が始まります。Ｚ会の小学２年生コースでは、つまずきやすい九九の勉強において、暗記をすることよりも｢意味理解｣に重点を置くことで、必要な場面で九九を適用する力や、今後の学習の基礎となる確かな力、学習指導要領をこえた発展問題を解く力を育みます。

Ｚ会の算数で特に重視するのは、「意味理解」です。つまり、数を数えるにしても、計算をするにしても、やり方の単なる暗記・覚えこみをめざすのではなく、意味や考え方をしっかりと理解したうえでそれらの力を身につけていくことに重きを置いています。	文章題の難しさは、問題文を読んで何算かを判断するところにあります。的確な判断をするためには、読解力・思考力・応用力などを要します。Ｚ会では文章題を重点的に取り上げることでお子さまの考える力を育成します。



暗記だけでなく確かな意味理解をすることによって、教科書の範囲を超えた発展・応用問題を解く力が育まれるため、Ｚ会では積極的に発展問題も取り上げています。	文章題の難しさは、問題文を読んで何算かを判断するところにあります。的確な判断をするためには、読解力・思考力・応用力などを要します。Ｚ会では文章題を重点的に取り上げることでお子さまの考える力を育成します。

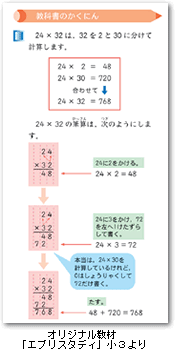
Z会では、計算の仕方だけでなく、「どうしてそうなるか」から解説します。また、発展問題で学力を充実させ、次学年へつなげます。

		何十、何百のかけ算の考え方や、位ごとに分割して考える方法など、筆算の根底にある考え方を図を用いて説明。
		かけ算の筆算の手順をわかりやすく解説。正確に計算する上でのアドバイスや工夫も紹介します。
		現在の教科書では一部しか扱っていない、かけられる数が4けたのかけ算、かける数が3けたのかけ算も解説・出題します。

		何十でわるときはどう考えればよいか、から、かんたんな形の2けたでわるわり算を扱い、考えさせます。
		商の見当のつけ方をはじめ、商の位がどこから立つかなど、手順をわかりやすく解説。また、注意すべきところや、わり算の性質を用いた計算の工夫なども示します。
		わり算を用いて解く発展問題を提示、詳しく解説。5年生の「割合」の学習にもつながっていきます。


	難しい単元でも、解き方のコツをつかむ。５年生算数の履修範囲の中で最もつまずきやすい単元は、「割合」です。Z会では、「割合」を学習する際に、すべて「（比べられる量）は（もとにする量）の（割合）」の形で把握してから、公式に代入する方法ですすめていきます。こうすることで「割合」の文章題を解くコツがつかめるようになり、消費税を扱った応用問題などにも取り組めるようになります。（註：一部の教科書では、「比べられる量」を「比べる量」としています）
	将来学ぶ「関数」の素地となる「比例」。秋～冬に学習する「比例」は、中学以降の数学で比重の高い「関数」分野の学習の素地となる大切な単元です。今のうちに「比例」の理解を深めておくことが、「関数」の学習をスムーズにする必須条件。Ｚ会では、「比例」を深く理解するために、次のような点に配慮して教材を作成します。比例の関係を式で表す際、中学で学習するy＝ａｘに準じて、○＝（きまった数）×□という形を用い、式で表す問題を多く扱います。関数で重要なグラフの見方を重視。２つのグラフを同時に扱う問題も出題します。

トップページ

入試で差がつく